
The algorithm shown in the Matlab section determined the most efficient sequence to collect all the debris. For a Δt of 1 hour between each capture, the most efficient sequence was (in order): Debris #5, Debris #4, Debris #2, Debris #3, and finally Debris #1. The least efficient (maximum ΔV) sequence was: Debris #3, Debris #5, Debris #1, Debris #2, and finally Debris #4. The results are tabulated below in Table 3.
Results

Table 3: Mission ΔV Analysis
Looking at Table 3, the most efficient sequence requires a ΔV of 5083.109 m/s. On the other hand, the least efficient trajectory uses a ΔV of 18267.747 m/s. This is a difference of 13184.638 m/s. The majority of the impuslive burns were performed in the x and z-direction.
The initial states of the orbital debris, with respect to the satellite in the Hill frame is shown below in Fig. 8.
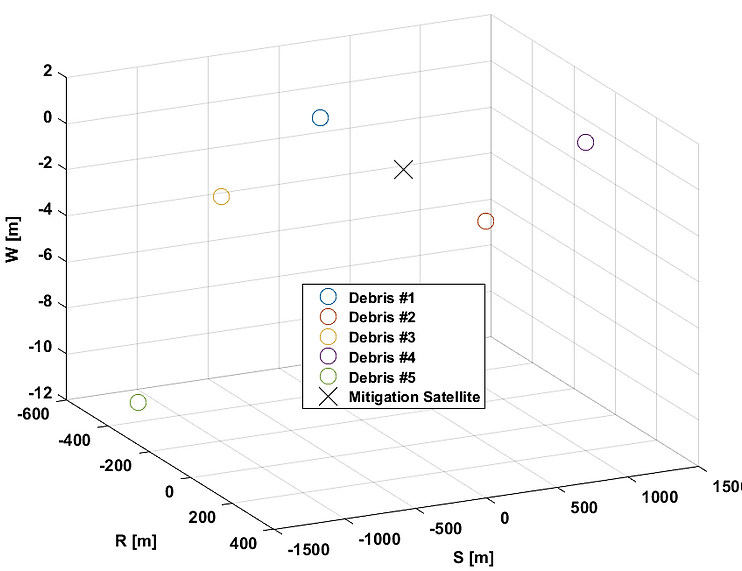
Figure 8. Initial Positions of Debris in Hill Frame
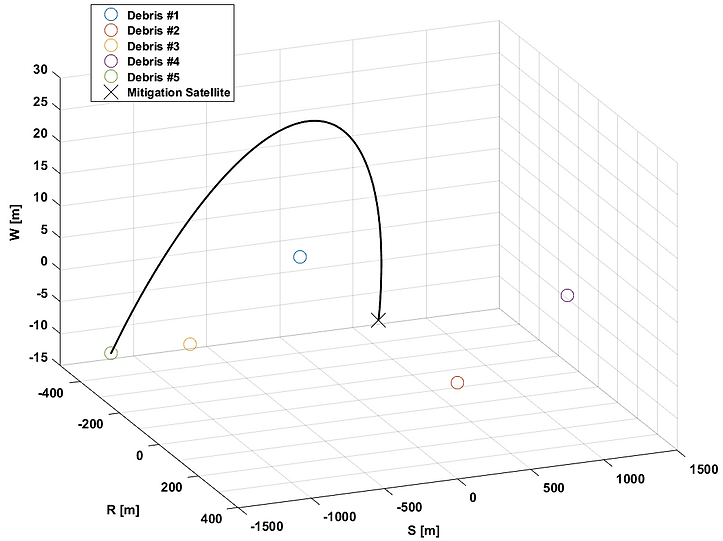
For validation, the satellite was propagated for 1 hour to see its trajectory. Beginning from the origin, the satellite ends up at Debris #5, the first target in the minimum ΔV sequence. This can be seen in Fig. 9 below. The trajectory was determined from the initial position of Debris #5 and the rendezvous velocity. It can be seen that the debris follows a parabolic trajectory with respect to the satellite. Since the analysis required a two-body propagation in the ECI frame, only the first capture trajectory was considered in the Hill frame.
Conclusions
Figure 9. Debris #5 Initial Capture Trajectory
For centuries to come, new satellites will continually orbit Earth as they are imperative to communication, astronomy, weather monitoring, navigation, remote sensing, and many more applications. However, we cannot keep playing this game of “dodgeball”. This analysis provided a fundamental understanding on how to mitigate multiple debris in a single mission. For these types of missions, debris must be collected in a very specific order. Depending on the time alloted for the mission, the amount of fuel used can be reduced drastically.
Recommendations
In order to produce more accurate and precise ΔV calculations, one would need to consider many factors left out in this analysis. These factors include orbital perturbations such as J2, atmospheric drag, gravity gradient torques, solar radiation, etc. The analysis also neglected ΔVs needed to remain in the debris' orbit, to allot time for capture and removal. For a more detailed analysis, the astrodynamicists would need to consider the relative angular rates and torques between the satellite debris. Furthermore, the debris and satellite probably would not reside in perfectly circular orbits, this would need to be accounted for as well. Due to the limitations of the Hill equations, large time-steps and distances cause large discrepancies in ΔV calculations. The mission time for orbital debris mitigation can be much larger than 5 hours, since it is not generally a time-sensitive issue. Also, astrodynamicists could consider using parking orbits to target incoming debris and save abundant amounts of fuel. Overall, orbital debris mitigation is an interesting and complex problem that will challenge the skills for future astrodynamicists.